Я знав! Я знав що з цим світом щось не так і взагалі це все матриця. Тільки коли наш мозок це повністю усвідомить ми зможемо звільнитись від неї. Крім глюку матриці 2+2=5, про який я писав раніше, виявлено ще одну несумісність - виявляється всі існуючі трикутники є однаковими! Не вірите? Ось авторитетне доведення:

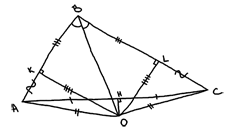
Нехай маємо довільний трикутник ∆ABC.
Проведемо серединний перпендикуляр до сторони AC, який перетинає її в точці H.
Проведемо з вершини B бісектрису. Вона буде перетинати серединний перпендикуляр у точці O. Тут є два варіанти - точка перетину може бути у трикутнику, або поза ним, як зображено на малюнках:

Варіант 1
Варіант 2

Для кожного з варіантів робимо наступні дії:

Проведемо з точки О перпендикуляри ОК і OL до сторін AB і ВС відповідно.
Розглянемо трикутники ∆ОНС та ∆ОНА. Вони рівні за двома сторонами та кутом між ними (ОН спільна, АН = НС бо ОН - серединний перпендикуляр, кути ∠ОНС та ∠ОНА обоє прямі). Звідси ОС = ОА.
Розглянемо трикутники ∆OLB та ∆ОКВ. Вони рівні за стороною і двома кутами (ОВ - спільна, кути ∠OLB та ∠ОКВ - прямі, кути ∠OBL і ∠OBK рівні бо ОВ - бісектриса). Звідси, BL = KB та OL=OK.
Розглянемо трикутники ∆OLC та ∆ОКА. Вони є прямокутними і рівними за гіпотенузою (ОС і ОА) і катетом (OL i OK). Звідси LC = AK.
Тепер BC = LC + BL = AK + KB = AB.
Звідки маємо, що трикутник рівнобедрений.

Аналогічно можна довести, що AB = AC, провівши серединний перпендикуляр до BC. Звідси випливає, що ∆ABC - рівносторонній! Отже будь-які трикутники є рівносторонніми і рівними між собою!

А знаєте що це означає? Саме так, the matrix has you!